As usual, the standard honor code and academic honesty policy applies.
computer science
Description
ACADEMIC HONESTY
As usual, the standard honor code and academic honesty policy applies. We will be using automated plagiarism detection software to ensure that only original work is given credit. Submissions isomorphic to (1) those that exist anywhere online, (2) those submitted by your classmates, or (3) those submitted by students in prior semesters, will be detected and considered plagiarism.
INSTRUCTIONS
In this
I. Introduction
II. Algorithm Review
III. What You Need To Submit
IV. What Your Program Outputs
V. Important Information
VI. Before You Finish
NOTE: This project incorporates material learned from both Week 2 (uninformed search) and Week 3 (informed search). Since this project involves a fair amount of programming and design, we are releasing it now to let you get started earlier. In particular, do not worry if certain concepts (e.g. heuristics, A-Star, etc.) are not familiar at this point; you will understand everything you need to know by Week 3.
The assignment's final due date is 04/25/2021, 23:30 UTC.
I. Introduction
An instance of the N-puzzle game consists of a board holding N = m^2 − 1 (m = 3, 4, 5, ...) distinct movable tiles, plus an empty space. The tiles are numbers from the set {1, …, m^2 − 1}. For any such board, the empty space may be legally swapped with any tile horizontally or vertically adjacent to it. In this assignment, we will represent the blank space with the number 0 and focus on the m = 3 case (8-puzzle).
Given an initial state of the board, the combinatorial search problem is to find a sequence of moves that transitions this state to the goal state; that is, the configuration with all tiles arranged in ascending order ⟨0, 1, …, m^2 − 1⟩. The search space is the set of all possible states reachable from the initial state.
The blank space may be swapped with a component in one of the four directions {‘Up’, ‘Down’, ‘Left’, ‘Right’}, one move at a time. The cost of moving from one configuration of the board to another is the same and equal to one. Thus, the total cost of path is equal to the number of moves made from the initial state to the goal state.
II. Algorithm Review
Recall from the lectures that searches begin by visiting the root node of the search tree, given by the initial state. Among other book-keeping details, three major things happen in sequence in order to visit a node:
- First, we remove a node from the frontier set.
- Second, we check the state against the goal state to determine if a solution has been found.
- Finally, if the result of the check is negative, we then expand the node. To expand a given node, we generate successor nodes adjacent to the current node, and add them to the frontier set. Note that if these successor nodes are already in the frontier, or have already been visited, then they should not be added to the frontier again.
This describes the life-cycle of a visit, and is the basic order of operations for search agents in this assignment—(1) remove, (2) check, and (3) expand. In this assignment, we will implement algorithms as described here. Please refer to lecture notes for further details, and review the lecture pseudocode before you begin the assignment.
IMPORTANT: Note that you may encounter implementations elsewhere that attempt to short-circuit this order by performing the goal-check on successor nodes immediately upon expansion of a parent node. For example, Russell & Norvig's implementation of breadth-first search does precisely this. Doing so may lead to edge-case gains in efficiency, but do not alter the general characteristics of complexity and optimality for each method. For simplicity and grading purposes in this assignment, do not make such modifications to algorithms learned in lecture.
III. What You Need To Submit
Your job in this assignment is to write driver.py, which solves any 8-puzzle board when given an arbitrary starting configuration. The program will be executed as follows:
$ python3 driver.py <method> <board>
The method argument will be one of the following. You need to implement all three of them:
bfs (Breadth-First Search)
dfs (Depth-First Search)
ast (A-Star Search)
The board argument will be a comma-separated list of integers containing no spaces. For example, to use the bread-first search strategy to solve the input board given by the starting configuration {0,8,7,6,5,4,3,2,1}, the program will be executed like so (with no spaces between commas):
$ python3 driver.py bfs 0,8,7,6,5,4,3,2,1
IMPORTANT: The version of the python that we are using is Python 3.6.4.
IV. What Your Program Outputs
When executed, your program will create / write to a file called output.txt, containing the following statistics:
path_to_goal: the sequence of moves taken to reach the goal
cost_of_path: the number of moves taken to reach the goal
nodes_expanded: the number of nodes that have been expanded
search_depth: the depth within the search tree when the goal node is found
max_search_depth: the maximum depth of the search tree in the lifetime of the algorithm
running_time: the total running time of the search instance, reported in seconds
max_ram_usage: the maximum RAM usage in the lifetime of the process as measured by the ru_maxrss attribute in the resource module, reported in megabytes
Example #1: Breadth-First Search
Suppose the program is executed for breadth-first search as follows:
$ python3 driver.py bfs 1,2,5,3,4,0,6,7,8
Which should lead to the following solution to the input board:
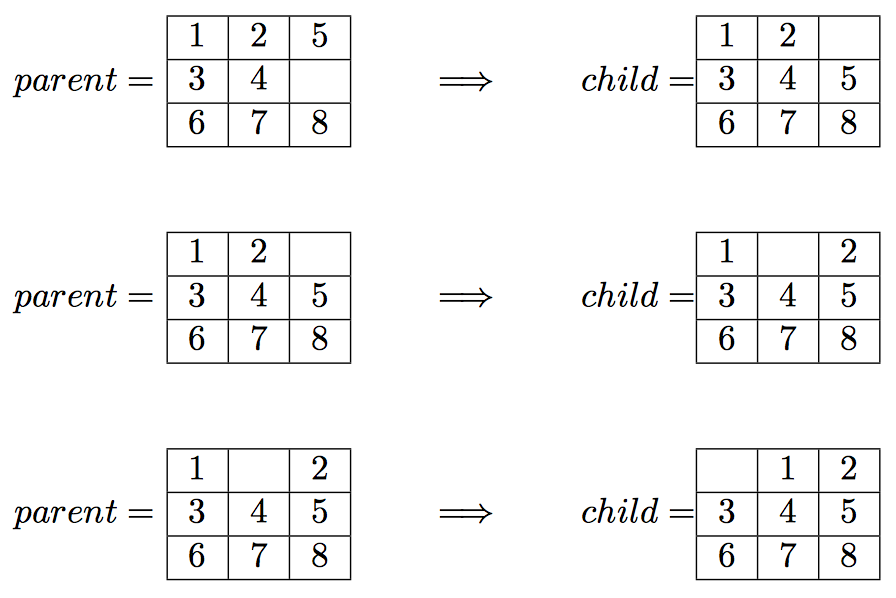
.
The output file (example) will contain exactly the following lines:
path_to_goal: ['Up', 'Left', 'Left']
cost_of_path: 3
nodes_expanded: 10
search_depth: 3
max_search_depth: 4
running_time: 0.00188088
max_ram_usage: 0.07812500
.
Example #2: Depth-First Search
.
Suppose the program is executed for depth-first search as follows:
$ python3 driver.py dfs 1,2,5,3,4,0,6,7,8
Which should lead to the following solution to the input board:

.
The output file (example) will contain exactly the following lines:
path_to_goal: ['Up', 'Left', 'Left']
cost_of_path: 3
nodes_expanded: 181437
search_depth: 3
max_search_depth: 66125
running_time: 5.01608433
max_ram_usage: 4.23940217
.
Other test cases are available on Week 2 Project: Implementation FAQs page.
Note on Correctness




