Mathematics is all around the world, you can’t skip mathematics even in a day. Whatever we do in a day involves maths. This is why mathematics is very essential in our day-to-day life and we can’t even imagine a day without maths. The word mathematics has originated from the term ‘Mathema’ which means Science or knowledge. Generally, mathematics is written as Math or Maths. There have limited branches of mathematics but with time maths and its branches have evolved.
Mathematics has made considerable contributions especially in the field of technology. Thus, there are several important branches of mathematics starting from the basic to the advanced level. But many students face difficulty in understanding the different branches of maths.
How Many Branches Of Mathematics Do We Have?
Table of Contents
Algebra, number theory arithmetic, and geometry are the five main fields of mathematics. Different specializations have emerged from these ancient branches of math, such as probability and statistics, topology, matrix algebra, game theory, and operations research, to name a few. Read this blog to learn everything there is to know about several mathematics disciplines, including a list and more.
List Of Most Important Branches Of Mathematics
These are the following most important branches of mathematics.
| Important Branches Of Mathematics |
| Pure mathematics |
| Arithmetics mathematics |
| Algebra maths |
| Geometry |
| Topology |
| Physics |
| Trigonometry |
| Probability and statistics |
| Calculus |
| Logic |
| Number theory |
Important Branches Of Mathematics Tree
These are the following major branches of the mathematics given in the below given tree.
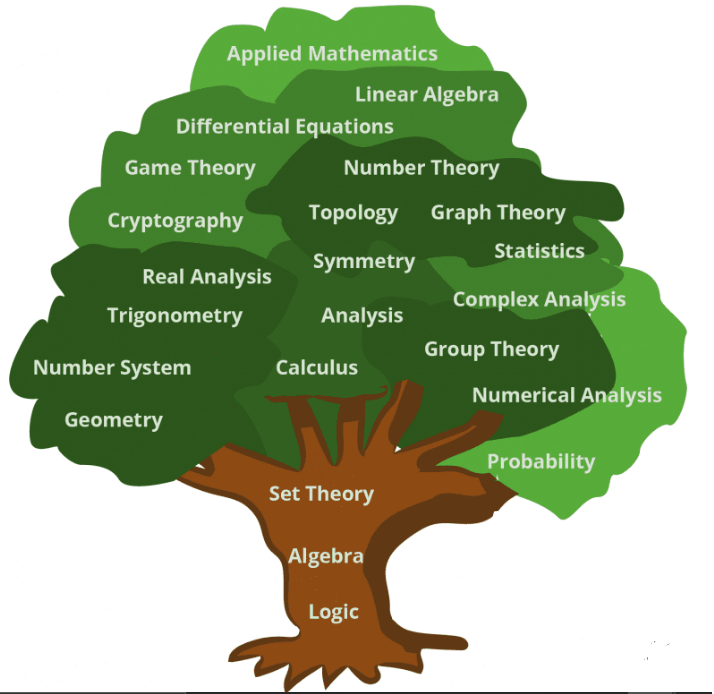
Pure Mathematics
It is the basic branch of maths which deals with the basic mathematical concepts. It is generally independent of any kind of application outside the maths. Pure math applies the maths concepts in the real world situations.
Here is the list of branches of Pure Mathematics.
| Branches Of Pure Mathematics |
| Algebra |
| Number Theory |
| Geometry |
| Arithmetic |
| Topology |
| Combinatorics |
| Mathematical Analysis |

Arithmetic Mathematics
The oldest branch of mathematics is arithmetic. It’s used to work with numbers ranging from 0 to 9, even odd, prime, or anything else. It includes the basic operations of addition, subtraction, multiplication. Everyone, from students to working professionals, uses arithmetic. also, we use it in our daily lives to conduct fundamental calculations. Pure mathematics is built on this foundation.
Let’s look at an example of a simple arithmetic formula and the example that goes with it. The average of the given number is calculated using the formula below.
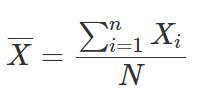
Algebra Maths
It is the most favourite mathematics branch for students as all the students enjoy working on algebraic expressions. It is one of the crucial branches of pure mathematics. In algebraic expressions, we use English alphabets to denote the algebraic values.
We use the algebra to find out the missing or unknown value in algebraic expressions or equations. Algebra does not only include algebraic equations. it has many more like other rules of operations, polynomial equations etc.
It also has subparts and elementary algebra is very famous for them. Generally we use elementary algebra for numbers representation. We can apply algebra in several structures like rings. We can say that it deals with symbols and states the rules of operating such symbols.
It has a many algebraic formulas to solve the algebraic equations.
In algebraic expression, we have variables which are represented in English letters and whose values we need to find out such as x, y, z etc.
Example of an algebra equation is 2x + 3y = 5.
Geometry
The next branch of mathematics is Geometry. It would not be wrong to say that it is the most practical mathematical branch in the world. You can check the applicability of geometry in real life and that too in day to day operations. It includes different shapes, sizes, figures and their properties and importance.
You will learn functioning of points, lines, angles, different types of surfaces, shapes and other solids etc. The best practical application of geometry you can see is that we all use geometry in GPS for finding ways. It is also used by manufacturing industries.
Topology
like geometry, there is one more branch with the name topology and it is an extensive form of geometry only. We use this branch to study the properties of shapes which cannot be changed even though their figure dimensions change.
Physics
If you have ever studied physics then you must be knowing the usage of maths in physics. You can solve many physics problems with the help of mathematics.it uses concepts of mathematics in physics ate derivatives, integration, differentiation etc. Thus many maths and physics concepts are similar and their foundations are also the same.
Trigonometry
If you ask any mathematical student about trigonometry, then they will say it is very tough. The word trigonometry is made up with two Greek words that are trigon which means triangle and second word is metron which means to measure. When the other branches of maths failed to solve the mathematical problems then we developed Trigonometry for the same.
It is the study of angles and triangles and it states the relation between such angles and sides of triangles.
It also studies geometry.
You will read different types of triangles like acute, right angle etc.
The following are some basic trigonometric formulas:
| Function | Property | Mathematical value |
| Sin a | opposite/hypotenuse | |
| Cos a | adjacent/hypotenuse | |
| Tan a | opposite/adjacent | Sin a/ cos a |
| Cosec a | 1/opposite/hypotenuse | 1/sin a |
| Sec a | 1/adjacent/hypotenuse | 1/cos a |
| Cot a | 1/opposite/adjacent | 1/ tan a |
Probability and statistics
Probability and statistics are an abstract branch of mathematics that uses mathematical principles to predict events that are likely to happen as well as organise, analyse, and interpret a set of data. It is one of the more recent branches of mathematics that has grown necessary due to its applications in both scientific and social sciences. This section is concerned with the laws and principles that control numerical data and random events. Statistics and probability are a branch of mathematics that is full of surprises.
Calculus
The next branch of mathematics is Calculus. Issac Newton and Gottfried Leibniz developed the Calculus in the 17th century. It studies the instant rate of change in calculations. You can sum the small factors and thus can find the whole number.
You must have heard of limits, functions, integrals, derivatives, integration etc. All these concepts come under the purview of Calculus. Calculus has two types that are differential calculus and integral calculus.
You can use the calculus concepts in science, engineering and in economics also.
Logic
The next branch of mathematics is Logic and it deals with the valid reasoning using different mathematical logics.
Number Theory
The next branch is Number theory and it is used with the positive integers and its properties. You can also study the relationship between different integers.
Advanced Branches Of Mathematics
Other advanced branches are subsets of the significant branches listed above. These branches are studied at a high level and entail complicated concepts that need solid computational abilities. The following are some of the more advanced branches.
Here are the ten branches of mathematics:
- Complex numbers
- Operations research
- Numerical analysis
- Matrix algebra
- Game theory
- Set theory
- Calculus
- Combinatorics
- Cartesian geometry
- Analysis
Branches Of Applied Mathematics
Applied mathematics combines mathematical concepts with the applications of various other fields. It’s the application of mathematics in combination with specialized expertise.
Here are the branches of applied mathematics.
| Branches of Applied Mathematics |
| Statistics and Probability |
| Set Theory |
| Calculus |
| Trigonometry |
Why Is Math So Hard?
When it comes to math and difficulty, we’ve established a few things:
- Math appears to be tough because it requires time and effort.
- Many students may not have enough time to “understand” arithmetic lessons and fall behind as the teacher progresses.
- Many students progress to increase complicated topics with flimsy foundations.
- We end up with a shaky building that will collapse.
This may appear to be bad news, but it is actually very excellent news. If we’re patient enough, the solution is simple!
You can succeed in math no matter where you are in your studies if you go back far enough to solidify your foundation. You’ll need to fill in the gaps with a thorough understanding of the fundamental ideas you learned in middle school arithmetic.
If you’re still in middle school, don’t try to go on until you’ve understood pre-algebra ideas. If necessary, get a tutor.
Download a middle school math curriculum or get a tutor if you’re high school and suffering with math. Make certain you comprehend every subject and action covered in middle school.
Top 10 Mathematics Universities In The World Of 2023
These are the following top mathematics universities in the world.
| Top Mathematics Universities In The World | Country |
| Stanford University | United States, Stanford |
| Massachusetts Institute of Technology (MIT) | United States, Cambridge (U.S.) |
| Princeton University | United States, Princeton |
| University of Cambridge | United Kingdom, Cambridge (U.K.) |
| Harvard University | United States, Cambridge (U.S.) |
| University of California Berkeley | United States, Berkeley |
| Universite de Paris | France, Paris |
| University of Oxford | United Kingdom, Oxford |
| ETH Zurich | Switzerland, Zurich |
| Sorbonne Universite | France, Paris |
Conclusion (Branches Of Mathematics)
We are always afraid of mathematics and thus, we do not value it although it is the most important part of our daily life as we use the practicality of mathematics in daily life. The number of Branches Of Mathematics is n and we are always confused between them. We hope this article has dispelled your doubts. If you have difficulty understanding these concepts or the difference between them, you can contact our experts at any time through Math homework help.
Frequently asked questions (FAQ)
What are the most complex branches of mathematics?
Algebra is the most challenging branch of mathematics. Abstract algebra is the most challenging part because it encompasses complex and infinite spaces.
Who is the father of mathematics?
The father of mathematics is Archimedes. He lived from 287 to 212 BC.
Who invented math?
It’s challenging to identify the actual beginnings of mathematics. So Pythagoreans are thought to have invented mathematics in the early sixth century. The axiomatic approach, which consists of a definition, axiom, theorem, and proof, Euclid introduced.



