Description

Introduction

Tablut is one of the family of tafl (or hnefatafl) games: Nordic and Celtic strategy games played on checkered boards between two asymmetric armies. These are ancient games, possibly related to the Roman game ludus latrunculorum, that were generally displaced by chess in the 12th century. Tablut is a variant from Lapland (the northernmost region of Finland). The detailed rules of these games are generally disputed; tablut, having survived into the 1700s, is perhaps best documented (by none other than Carl Linnaeus, the fellow responsible for our state animal being known as Ursus arctos californicus and our state trees as Sequoia sempervirens and Sequoiadendron giganteum in scientific circles). However, his account is itself incomplete and additional confusion resulted from the later mistranslation of his manuscript from Latin. Therefore, any of you familiar with modern reconstructions of the game should not expect that our version will be identical to yours.

Tablut is played on a 9x9 checkerboard between a set of 9 white pieces and 16 black pieces. The middle square is called the throne (or castle). One of the white pieces is the king, and the others, his guards, are known as Swedes. The white side wins if the king reaches one of the edges of the board. The black pieces are known as Muscovites (referring to the Grand Duchy of Moscow). Their aim is to capture the king before he reaches the edge of the board.

 

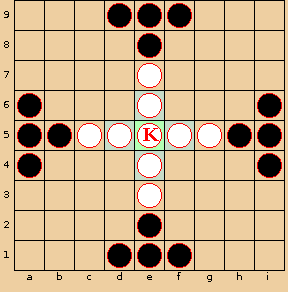
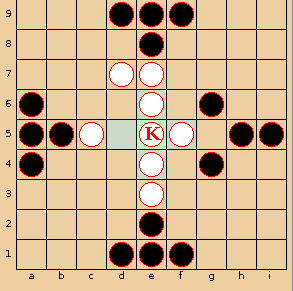
Figure 1. On the left: a Tablut board showing the standard numbering of squares, and the initial placement of the pieces. On the right: the board that results after the three moves i6-g, d5-7, i4-g (the last move is a capture).

All pieces move like chess rooks: any number of squares orthogonally (horizontally or vertically). Pieces may not jump over each other or land on top of another piece. No piece other than the king may land on the throne, although any piece may pass through it when it is empty. The black (Muscovite) side goes first.

A piece other than the king is captured when, as a result of an enemy move to an orthogonally adjacent square, the piece is enclosed on two opposite sides (again orthogonally) by hostile squares. A square is hostile if it contains an enemy piece, or if it is the throne square and is empty (that is, it is hostile to both white and black pieces). The occupied throne is also hostile to white pieces when three of the four squares surrounding it are occupied by black pieces. Captures result only as a result of enemy moves; a piece may move so as to land between two enemy pieces without being captured. A single move can capture up to three pieces.

The king is captured like other pieces except when he is on the throne square or on one of the four squares orthogonally adjacent to the throne. In that case, the king is captured only when surrounded on all four sides by hostile squares (of which the empty throne may be one).

A side also loses when it has no legal moves on its turn, or if its move returns the board to a previous position (same pieces in the same places and the same side to move). As a result, there are no drawn games.